corCTF 2025 purely-functional-oop: Compiling object-oriented code into Google Sheets expressions
corCTF 2025 - purely-functional-oop
This blog was also posted to the Crusaders of Rust website.
This challenge is the culmination of my adventures with Google Sheets functional programming. In part one, I implemented church numerals and arithmetic using only pure lambda abstractions and applications, and in part two, I outlined a framework upon which smalltalk-style object-oriented message passing could be implemented. For corCTF 2025, I decided to implement those ideas into an actual product, compiling a custom object-oriented language into an executable Google Sheets formula.
Players were provided the source code for the compiler and were given access to a server running the same code, bound to the real flag. In order to solve this challenge, players had find a vulnerability in the compiler and submit code in the object-oriented language that, when compiled and executed, would reveal the flag.
I thought this challenge was really cool and allowed players to experiment with compilers in a new context without getting too deep into advanced concepts. In this blog, I will talk about the design of this compiler as well as the intended solution for this ctf challenge.
The Language
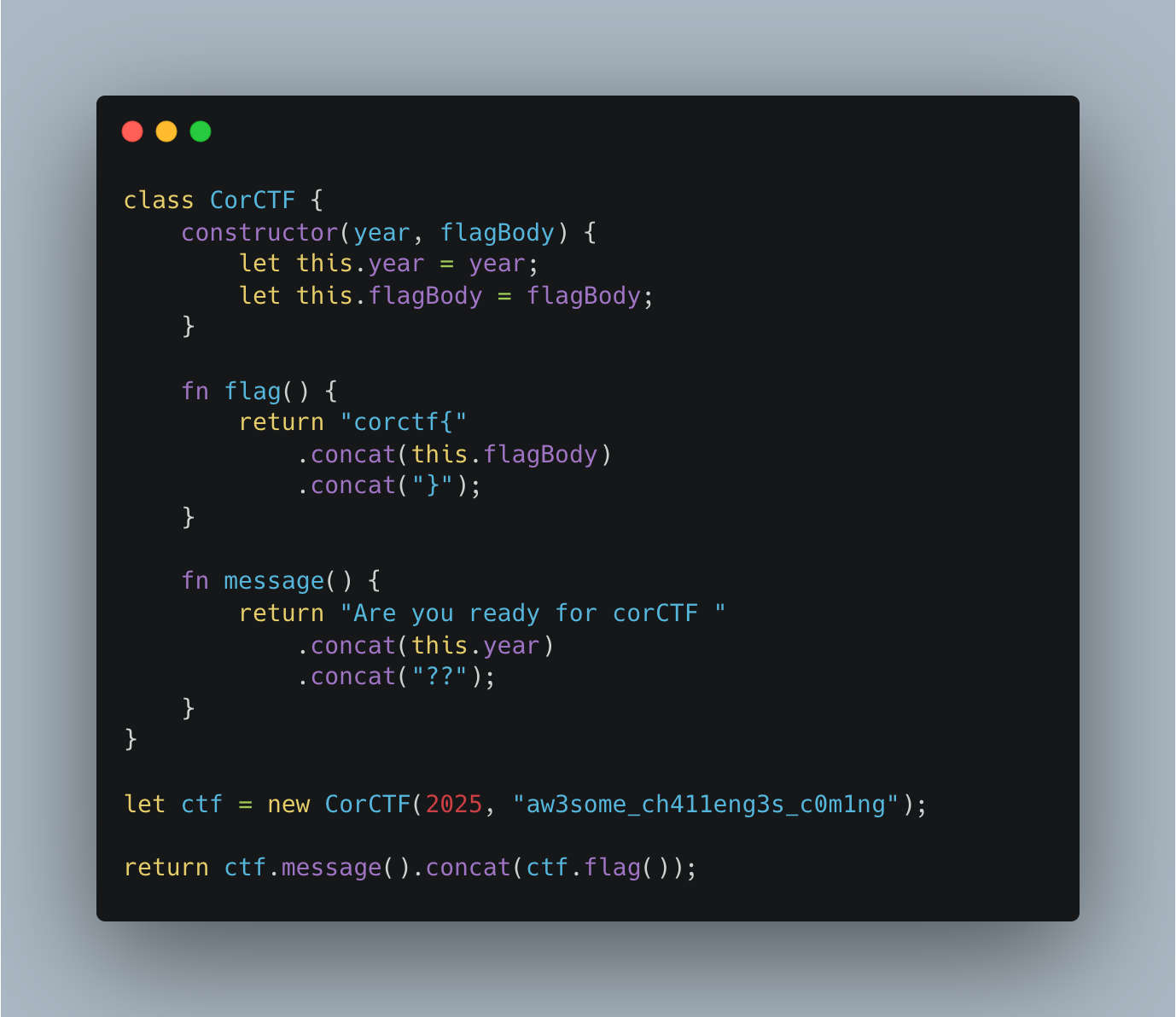
From the teaser, we get a basic demonstration of the features in the language. This is a pure object-oriented language, users can declare classes with constructors that assign instance fields, as well as methods. All values in the language are objects, even the built-in integer and string literals (which are wrapped with methods).
The code would then be automatically compiled into a google sheets formula, which would be executed in a cell.
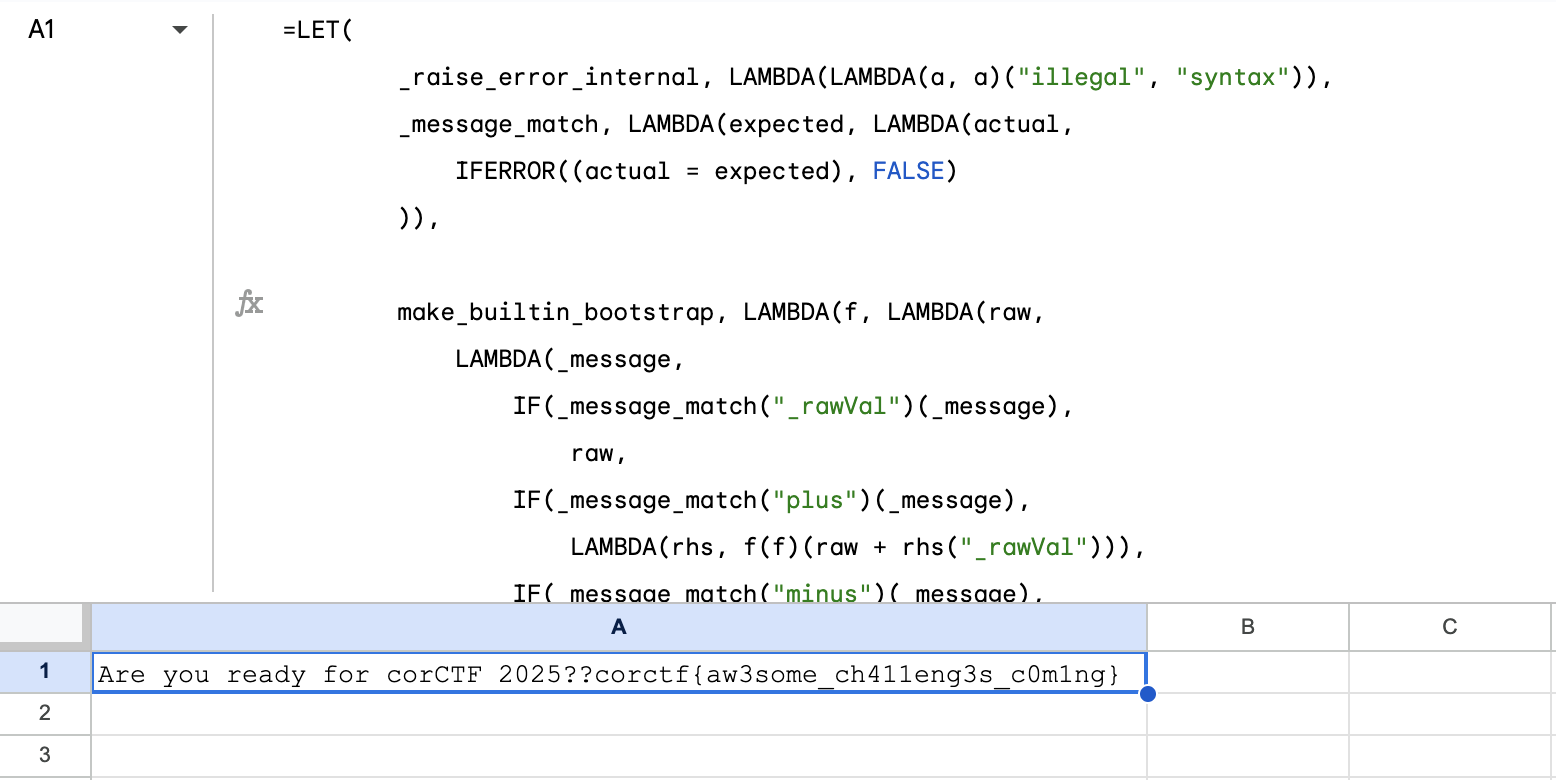
In the service itself, we see that our submitted code is also linked with another class declaration, which gives users a chance to obtain the flag:
"""
class Challenge {
constructor() {
let this.n = 3;
let this.flag = """ + f'"{FLAG}"' + """;
}
fn verifySolution(a, b, c) {
let nonzeroInput = nonzero(a).and(nonzero(b)).and(nonzero(c));
let integerInput = isInteger(a).and(isInteger(b)).and(isInteger(c));
let satisfiesTheorem = pow(a, this.n).plus(pow(b, this.n)).equals(pow(c, this.n));
let accepted = nonzeroInput.and(integerInput).and(satisfiesTheorem);
return accepted ? this.flag : "Solution rejected";
}
}
"""
This code requires users to enter three nonzero integers that can satisfy Fermat’s Last Theorem for n=3. Unfortunately, it has already been proven that no solutions exist for this mathematical problem — in order to get the flag, solvers would need to hack the compiler to trick the program.
The Compiler
This compiler was hastily written, so the exact terminologies used in the internal documentation may be inaccurate.
In order to compile code, the program uses python’s lark library to parse the language’s grammar, and then uses a recursive algorithm to generate the formula substitutions for each node in the parse tree. The grammar defines four types of statements: class definitions, function definitions, constructor definitions, and instructions (class assignment, assignment, and return statements). Functions could be defined either statically (outside of any class), or as an instance method (inside of a class). For simplicity, nested classes were not allowed in the language.
The recursive algorithm would generate the Google Sheets formula substitution, resolving each subtree until finished. For example, a method call would boil down to this expression:
args = ", ".join(parse_expression(arg, scope, outer_name) for arg in argument_list.children)
if not args:
return f"{callee}(\"{method_name}\")" # no curried arguments
else:
return f"{callee}(\"{method_name}\")({args})"
In hindsight, it would’ve made more sense to make parameterless lambdas for no-argument methods. I didn’t know that existed at the time.
Otherwise, assignments and declarations would resolve into a string and expression pair that could be
combined inside of a Google Sheets LET expression.
elif statement_type == "assignment":
variable_name = statement.children[0]
ensure_valid_name(variable_name)
rhs = parse_expression(statement.children[1], scope, outer_name)
return (f"{variable_name}, {rhs},\n", False)
Things start to get a little complicated when we declare classes. We want both this and the original class
to be available inside method calls, but in lambda calculus, explicit recursion isn’t possible. In order to
implement this, I wrote this monstronsity of a template to handle double recursion:
# template for a class definition
compiled_result = f"""
class_{class_name}, LAMBDA(_constructor, LAMBDA(this,
{constructor_opening}
LAMBDA(_message,
{message_handler}
)
{constructor_closing}
)),
bootstrap_new_{class_name}, LAMBDA(_f,
LAMBDA({constructor_args_comma}
class_{class_name}(
LAMBDA({constructor_args_comma}
(LAMBDA(_message, _f(_f)({constructor_args})(_message)))
)
) (LAMBDA(_message,
_f(_f)({constructor_args})(_message)
)) ({constructor_args})
)
),
new_{class_name}, (bootstrap_new_{class_name}) (bootstrap_new_{class_name}),
"""
A similar, simpler recursive template was used to enable static function call recursion. For brevity, I won’t show it here.
All primitives are wrapped in objects with predefined methods for functionality. Internally, they are accessed using
the _rawVal method:
make_builtin_bootstrap, LAMBDA(f, LAMBDA(raw,
LAMBDA(_message,
IF(_message_match("_rawVal")(_message),
raw,
IF(_message_match("plus")(_message),
LAMBDA(rhs, f(f)(raw + rhs("_rawVal"))),
IF(_message_match("minus")(_message),
LAMBDA(rhs, f(f)(raw - rhs("_rawVal"))),
IF(_message_match("times")(_message),
LAMBDA(rhs, f(f)(raw * rhs("_rawVal"))),
IF(_message_match("divide")(_message),
LAMBDA(rhs, f(f)(raw / rhs("_rawVal"))),
IF(_message_match("equals")(_message),
LAMBDA(rhs, f(f)(raw = rhs("_rawVal"))),
IF(_message_match("notEquals")(_message),
LAMBDA(rhs, f(f)(raw <> rhs("_rawVal"))),
IF(_message_match("and")(_message),
LAMBDA(rhs, f(f)(AND(raw, rhs("_rawVal")))),
IF(_message_match("or")(_message),
LAMBDA(rhs, f(f)(OR(raw, rhs("_rawVal")))),
IF(_message_match("xor")(_message),
LAMBDA(rhs, f(f)(XOR(raw, rhs("_rawVal")))),
IF(_message_match("lessThan")(_message),
LAMBDA(rhs, f(f)(raw < rhs("_rawVal"))),
IF(_message_match("lessThanOrEquals")(_message),
LAMBDA(rhs, f(f)(raw <= rhs("_rawVal"))),
IF(_message_match("greaterThan")(_message),
LAMBDA(rhs, f(f)(raw > rhs("_rawVal"))),
IF(_message_match("greaterThanOrEquals")(_message),
LAMBDA(rhs, f(f)(raw <= rhs("_rawVal"))),
IF(_message_match("negate")(_message),
f(f)(NOT(raw)),
IF(_message_match("factorial")(_message),
f(f)(FACT(raw)),
IF(_message_match("log")(_message),
f(f)(LOG(raw)),
IF(_message_match("concat")(_message),
LAMBDA(rhs, f(f)(CONCAT(raw, rhs("_rawVal")))),
_raise_error_internal()
))))))))))))))))))
)
)),
make_builtin, (make_builtin_bootstrap) (make_builtin_bootstrap),
Being derived from a functional programming language, everything here is immutable and pure. This means that repeated method calls on an object must always return the same value. Since there is no mathematical solution to the constraints, what inputs can we pass to the challenge to get the flag?
The Exploit
The compiler has a set of reserved keywords in order to prevent names from overlapping with other tokens used in the system. These are the keywords:
RESERVED_KEYWORDS = {
"class", "fn", "constructor", "let", "return",
"new", "this", "true", "false", "_f", "_message",
"_constructor", "_message_match", "_raise_error_internal"
}
Since there is no runtime type checking in this programming langauge,
numbers behave just like
any other object — There is actually nothing preventing us from
writing custom number objects that define all those same methods.
Notice that the _rawVal method isn’t a reserved keyword, so we can call and implement these methods
on any system. My intended solution abuses this mechanic by creating a special
boolean value that will always return the same truth value, no matter what
logical methods are called from it. This code yields the flag, corctf{p0lym0rpHic_fr33k_1n_th3_sh33ts}
class TrapBoolean {
constructor(inner) {
let this.inner = inner;
}
fn _rawVal() {
return this.inner._rawVal();
}
fn and(other) {
return this;
}
}
class TrapNumber {
constructor(inner) {
let this.inner = inner;
}
fn _rawVal() {
return this.inner._rawVal();
}
fn notEquals(other) {
return new TrapBoolean(true);
}
}
let chall = new Challenge();
return chall.verifySolution(new TrapNumber(0), 0, 0);
The CTF
Unfortunately, this challenge had unintended solutions which took advantage of
Google Sheets’ type confusion, with the one-line exploit
return new Challenge().verifySolution("0", "0", "0");.
As my friend Drakon accurately pointed out, “this is why we need a strongly typed spreadsheet.”
At least some teams found the intended solution! I’d like to shout out the team
Squid Proxy Lovers for taking the time to write up their analysis and solution, which actually took advantage
of the language and compiler features.
The Conclusion
Despite compiling to a platform with a completely different programming paradigm,
the intended solution for this challenge does not involve any mechanics specific to Google Sheets.
purely-functional-oop serves as a warning against the dangers of duck typing and polymorphism.
I loved playing with this new concept and exploring the relationship between functional and object-oriented programming. Even though there was a cheese to the challenge, creating a compiler for this challenge and playing with Google Sheets formula technology was a lot of fun. Although there is very little practical usage in bringing object-oriented programming into spreadsheets, I found it interesting nonetheless. Who knows, maybe some tinkerer in the future will develop this concept into a proper toolchain.